So Really, What is a Word?

The Shape of a Word and How Language Creates Geometry in Our Minds and Machines

So what is a word?

In a dictionary, we get several definitions, and hundreds of words to describe ‘word’. So a word is maybe more than meets the eye. In this article we’ll explore this question right from the very beginning and demonstrate that a word is rooted not as an abstract symbol but in in the physics of the observable world. Buckle up, and be ready for a different linguistical journey.

A word as we mostly consider it

At first glance, a word is just letters on a page, a symbol we agree has meaning. But this view misses the fundamental truth that long before writing or glyphs, a word was a sound. And that sound is a vibration launched into the air, a complex pressure wave, a fleeting piece of acoustic magic. Then connected in speech, words form a song with rhythm, cadence, and beat and even melody.

This physical perspective, grounded in the sounds and rhythms of speech now connects us to mathematics shapes and even and importantly geometry. This is not something that comes easily to the mind and our everyday context. However, rooted in, well understood mathematical theory it offers a new way to think about language. And here we find a hidden geometry in our words and as we delve deeper it suggests that the AI models now transforming our world have unknowingly stumbled upon this very same secret.

The Hidden Music of Speech

If we listen to someone speak, their voice rises and falls, speeds up and slows down, placing emphasis on certain syllables. This is called prosody: it is the natural rhythm, stress, and intonation of speech. Consider the simple act of asking a question: the rising intonation at the end of a sentence is what distinguishes a genuine inquiry from a flat statement. This vital nuance is part of the 'music' of speech, a piece of information that gets flattened into a single, static question mark on the page.

The music and rhythms of speech also prevents language from being a flat, robotic drone - maybe a tone that in writing you’ve noticed in output of LLMs, a ‘certain something’ that catches the flow as you read and, where em dashes often appear to stand in for conversational rhythm or missing words.

If we think this through we can see that this music isn’t just decorative, it part of the process of communication. When we hear a continuous stream of sound as in a sentence, or song, our brains perform a kind of "natural tokenization." We use a process of converting the sounds from acoustic pressure waves to stored in the weights of the synapsed in the neurones of our brains. In this complex process we then use the rhythmic pulses and pauses as cues to physiologically segment the audio into meaningful chunks like syllables and words. For example, a word like "pebble" isn't just a jumble of sounds; its acoustic waveform has a distinct two-part pulse that our brain use in the stored patterns in the neurones of our brains. So a sound is the native format of language: a dynamic, analogue signal rich with information.

Modern LLMs, however, never hear the sound of a word or the rhythms and music of speech and songs. They learn from text, and their method of tokenization is based on statistical frequency, not acoustic physics. Typically an algorithm like ‘Byte-Pair Encoding’ breaks words down based on common letter patterns in a massive dataset. This process is a "lossy approximation" of speech that can not capture all the prosody such as the rhythm, pitch, stress, and emotional tone. And in this process this it ‘flattens’ the rich signal into a sequence of static digital ‘tokens’ that may lose some of the nuances and tone of spoken language.

At the moment, this flattened sequence is the only input the AI has. And from this simpler representation, it must reconstruct the universe of human language and capture enough meaning in such a way we can see meaning when we read the output. The big question is how is that possible? It turns out, the answer appears to lies in geometry.

Finding the Shape in the Sound

So, if a word is a complex signal, how can we see its underlying shape? This question isn't new and has been a subject of great interest in many field of study. However, importantly in the 1980s, scientists started studying complex systems, such as the chaotic rhythm of a human heart, the complex patterns of the signals of the brain and the unpredictable patterns of weather. And in studying thee signal measured from these systems developed a stunningly effective technique to do just that and so we move on to the next part of our journey into a landscape of words.

Phase-space Embedding - a Little Mathematical Magic

The core idea in phase-space embedding is elegantly simple. We’ll try and unravel it so you can get a sense of how it works. The first thing we do when we have a signal like the sound waves of a word or the electrical signal of a heart is we measure it and turn it into a regular sequence of values in time steps - this is a good approximation. This sequence is called a time series, a set of values in time. A sentence is also a set of values in time and we will come to that later. But let’s concentrate on the sound of a word or an ECG signal.

We call a time series signal like a sound or ECG, one-dimensional signal as we can plot it on paper as a graph as line. However, we can plot the same signal into two dimensions using the "method of delays". You plot the signal's value now against its value a fraction of a second ago. By repeating this process, you unfold the flat, linear signal into a trajectory in a two or even more dimensions, by repeating the process.

If we imagine measuring a ball with a single string we could only measure its circumference, a one-dimensional line. However, in two dimensions, we would see a circle and in three we would get the full picture, a sphere. Phase-space embedding does the same for a word’s sound, it folding the sound’s waveform into a multidimensional geometric shape.

So for complex signals like a sound wave or an ECG signal what appears as a noisy, one-dimensional line becomes a beautiful geometric object. And we call that a "system attractor". The word attractor has since slipped into modern language - but the history of the word has often been forgotten. The system attractor reveals the hidden structure of the system that created it. It’s called system because its the mathematics of the system define the shape of the attractor. The shape is made of ‘loops’, ‘spirals’, and ‘folds’ of this shape represent the system's underlying dynamics. Interestingly, these are the same words mysteriously slipping into the language used to describe LLMs.

The geometry of a spoken word

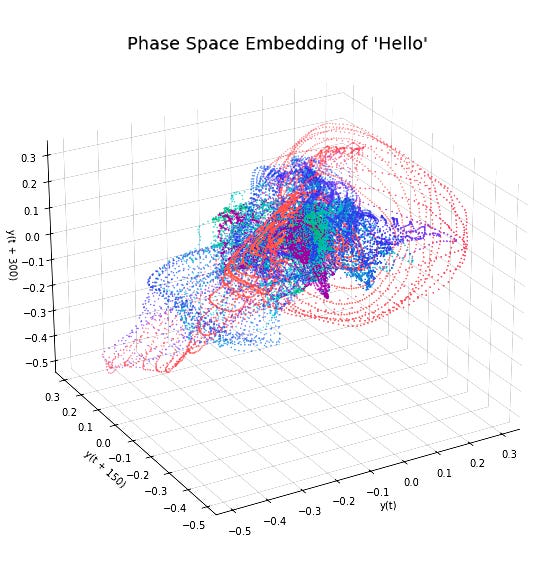
We can do the exact same thing with the sound of a spoken word. By embedding its acoustic waveform into phase space, we can see its unique geometric signature as seen in the figure below, the word 'hello' forms a distinct trajectory

So, this is the shape of a word, it is a trajectory through phase space, with every curve and corner defined by the physics of the human voice. This isn't a metaphor; it's a real mathematical reconstruction of a word's dynamic identity. This figure is a ‘hello’ to the very real geometry of words.

The Ghost in the Machine - Geometry in LLMs

Now here’s where the story takes a fascinating turn and this takes the process of turning a time series into geometry much further. The ‘Transformer’ architecture is the engine behind most modern LLMs, and when we look at how it works through the eyes of the mathematics of nonlinear dynamics we find it a appears to have unknowingly been built on the same geometric principle.

The core of the Transformer is a mechanism that its inventors called "attention". The mechanism’s aim was to turn time series data, these series of words, from a line of sequential data in to a two dimensional matrix. This matrix lets the model process language quickly using GPUs (Graphical processor Units), the same chips that power image calculations. So the semantic word used ‘attention’ was assigned for the process. However this name is a little misleading. The mechanism doesn't "attend" or "focus" in any cognitive sense. At its core, it is a machine for making systematic pairwise comparisons.

Mathematically, for any given sequence of tokens, the "attention" mechanism calculates a similarity score between every single token and every other token in the sequence, using the dot product of token representations which the designers again assigned descriptors that sound like they are doing something special: they called them called "queries" and "keys". However, the end result is a giant grid, or matrix, that maps out the relationship between all the parts, which can then be used to train a neural network. And importantly be done using a GPU for high speed calculations

Similarly, the attention mechanism's core function is to systematically compare a token at one position with the tokens at every other position, creating a relational map that reveals the sentence's latent geometry. This operation, is functionally analogous to the phase-space embedding we just explored. It is a method for taking a flat sequence and reconstructing its latent geometry. And so we can see the Transformer isn't "attending" to words; it is reconstructing a "language attractor," a vast, high-dimensional manifold where semantic and syntactic relationships are encoded as geometric trajectories.

This geometric principle extends beyond sound into the realm of language as processed by an AI. In an LLM, a word is not text but a rich numerical object called a vector. A sentence, therefore, becomes a sequence of these vectors, forming a path through a high-dimensional conceptual space. By applying the same "method of delays" to this sequence, we can visualize the sentence's trajectory. The figure below plots the state of a sentence at one point in time against its state at the next, revealing the geometric shape of an entire thought.

As we can see above a sentence is no longer a list of words; it is a path through this space - in this case “The quick brown fox jumps over the lazy dog happily today before tea”. Its meaning is not contained in the individual tokens, but in the overall shape of the journey. And then this journey is captured by the neural network.

Why This New Perspective Matters

Realizing that language, both in our heads and in our machines, has a geometric structure is more than just a piece of interesting trivia it becomes clear it has profound implications:

Towards Better Interpretability

Now we have this new perspective we can think of LLMs as geometric engines rather than black boxes. We can create a mental picture of what is going on. And having this new picture we can start to analyse their behaviour in a new light. For example, we can ask questions like, “What does the ‘democracy’ manifold look like?” or “Why did the model veer off course to give an odd answer?”

By seeing LLMs as geometric engines, we can trace their decision paths, making them less like black boxes. In this way we may be able take a crucial step toward more transparent and understandable LLM systems. In our previous work we could see how an LLM demonstrated behaviours of looping and divergence that we associate with nonlinear systems.

A New Road to Efficiency

Another interesting possibility is that this geometric view suggests parts of the Transformer, like positional encodings, might be redundant. In phase-space embedding, a trajectory’s shape captures temporal order naturally, hinting that leaner, more principled model designs could reduce computational costs. Clearly the current mechanism works very well however, taking into account geometry and using phase-space embedding to it’s full advantage may point to leaner, more efficient, and a more principled model designs

A New Philosophy of Language

Maybe one of the most profound implications of these ideas is that this perspective changes how we might think about ‘meaning’ itself. This view shifts language from abstract rules to a dynamic field. In our brains, meanings and paths are encoded in the neurone synapses. In an LLMs, the paths are stored in it’s neural network’s weights. Both are landscapes, and it seems the AI’s challenge is to navigate them as fluently as we do.

From this viewpoint we can see the words and sentences flow like a river along the hills and valleys. When we learn, just as an AI learns, we build up this landscape. Language was then never meant to be just text on a page it becomes a landscape to explore. The challenge for AI, and perhaps for us, is to rediscover the shape of our words and wander their vast and vibrant terrain.

Related work

Pairwise Phase Space Embedding in Transformer Architectures


Copyright © Kevin R. Haylett 2025